Algorithms
An algorithm is a set of steps of operations to solve a problem performing calculation, data processing, and automated reasoning tasks. An algorithm is an efficient method that can be expressed within finite amount of time and space. An algorithm is the best way to represent the solution of a particular problem in a very simple and efficient way. If we have an algorithm for a specific problem, then we can implement it in any programming language, meaning that the algorithm is independent from any programming languages
The word Algorithm means “a process or set of rules to be followed in calculations or other problem-solving operations”. Therefore Algorithm refers to a set of rules/instructions that step-by-step define how a work is to be executed upon in order to get the expected results.
Properties of Algorithm
All Algorithms must satisfy the following criteria -
1) Input There are more quantities that are extremely supplied.
2) Output At least one quantity is produced.
3) Definiteness Each instruction of the algorithm should be clear and unambiguous.
4) Finiteness The process should be terminated after a finite number of steps.
5) Effectiveness Every instruction must be basic enough to be carried out theoretically or by using paper and pencil For example,suppose you are cooking a recipe and you chop vegetables which are not be used in the recipe then it is a waste of time
6)Independent An algorithm should have step-by-step directions, which should be independent of any programming code. It should be such that it could be run on any of the programming languages
What are the Characteristics of an Algorithm
Performance Analysis of Algorithm
i) Time Complexity
ii)
Space Complexity
Analyzing Algorithm( Analysis of Algorithm)
To analyze a programming code or algorithm, we must notice that each instruction affects the overall performance of the algorithm and therefore, each instruction must be analyzed separately to analyze overall performance. However, there are some algorithm control structures which are present in each programming code and have a specific asymptotic
Some Algorithm Control Structures are:
1. Sequencing
2.If-then-else
3.for loop
4.While loop
Asymptotic Notation of Algorithm (Growth Functions)
Growth functions are used to estimate the number of steps an algorithm uses as its input grows
Asymptotic Notation is used to describe the running time of an algorithm - how much time an algorithm takes with a given input, n. Asymptotic Notation is a way of comparing function that ignores constant factors and small input sizes.
- It is a way to describe the characteristics of a function in the limit.
- It describes the rate of growth of functions.
- Focus on what’s important by abstracting away low-order terms and constant factors.
- It is a way to compare “sizes” of functions:
- O≈ ≤ Ω≈ ≥ Θ≈= o≈< ω≈>
1. They give simple characteristics of an algorithm's efficiency.
2. They allow the comparisons of the performances of various algorithms.
Three notations are used to calculate the running time complexity of an algorithm: There are three different notations:
big O,
big Theta (Θ),
big Omega (Ω)
1) Big-O Notation
The Big-O notation describes the worst-case running time of a program. We compute the Big-O of an algorithm by counting how many iterations an algorithm will take in the worst-case scenario with an input of N. We typically consult the Big-O because we must always plan for the worst case.
For example, O(log n) describes the Big-O of a binary search algorithm.
2) Big-Ω Notation
Big-Ω (Omega) describes the best running time of a
program. We compute the big-Ω by counting how many
iterations an algorithm will take in the best-case scenario
based on an input of N. For example, a Bubble Sort
algorithm has a running time of Ω(N) because in the best
case scenario the list is already sorted, and the bubble
sort will terminate after the first iteration.
3. Theta (θ) Notation:
The function f (n) = θ (g (n)) [read as "f is the theta of g of n"] if and only if there exists positive constant k1, k2 and k0 such that k1 * g (n) ≤ f(n)≤ k2 g(n)for all n, n≥ n0
Explanation
Recurrence relation
A recurrence is an equation or inequality that describes a function in terms of its values on smaller inputs. To solve a Recurrence Relation means to obtain a function defined on the natural numbers that satisfy the recurrence.
There are four methods for solving Recurrence:
1. Substitution Method
2. Iteration Method
3. Recursion Tree Method
4. Master Method
Masters theorem
| Time Complexity | |
|---|---|
| Best | O(n+k) |
| Worst | O(n+k) |
| Average | O(n+k) |
| Space Complexity | O(max) |
| Stability | Ye |
| Time Complexity | |
|---|---|
| Best | O(nlog n) |
| Worst | O(nlog n) |
| Average | O(nlog n) |
| Space Complexity | O(1) |
| Stability | No |
| Time Complexity | |
|---|---|
| Best | O(n*log n) |
| Worst | O(n*log n) |
| Average | O(n*log n) |
| Space Complexity | O(n) |
| Stability | Yes |
| Time Complexity | |
|---|---|
| Best | O(n*log n) |
| Worst | O(n2) |
| Average | O(n*log n) |
| Space Complexity | O(log n) |
| Stability | No |
Advance Data Structure
Graph Algorithm
Advance Design and Analysis Techniques
Dynamic programming is a programming technique where an algorithmic problem is broken down into subproblems
Parallel Algorithm
Why do we need parallel sorting?
The process of sorting a list of elements is fairly frequent. When we need to sort a sizable amount of data, a sequential sorting method could not be effective enough. Therefore, parallel algorithms are used in sorting.
What is the potential speed-up with parallel sorting?
If we talk about sequential sorting, its best complexity turns out to be O(nlogn). Using parallel sorting, if we have n processors, its optimal complexity turns out to be O(nlogn)/n = O(log n).
PRAM
NP Complete Problem
A decision problem is NP-complete if:
- is in NP, and
- Every problem in NP is reducible to in polynomial time.
can be shown to be in NP by demonstrating that a candidate solution to can be verified in polynomial time.
Only for self study
Searching Algorithm
Linear Structure
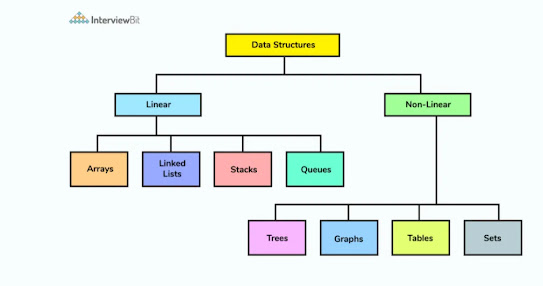







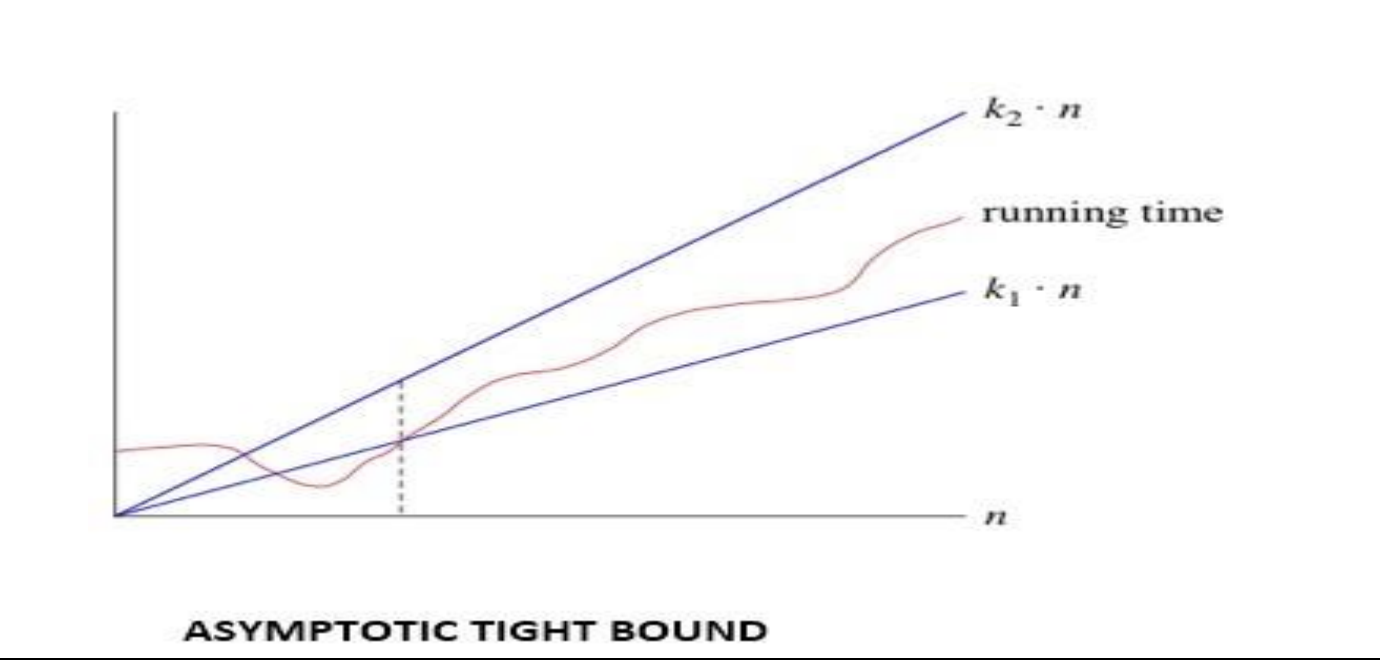










Above doc has all topic related to data structure and analysis of algo
ReplyDeletehttps://er.yuvayana.org/performance-analysis-of-parallel-algorithms/
ReplyDelete